Solucion a problemas de movimientos en 1-D y dos o tres dimensiones.
Mientras revisaba mis pasadas publicaciones me di cuenta de que había algunos problemas que había postulado pero que nunca trabajé en mostrar sus resultados. Así que aquí están las respuestas a esos problemas.
Movimiento en 1-D
- Un modelo de cohete se lanza hacia arriba. Su altitud y en función del tiempo viene dada por y = bt - ct2 + 5, donde b = 75 m/s, c = 3.7 m/s2, t es el tiempo en segundos e y está en metros. (a) Utilice la diferenciación para hallar una expresión general de la velocidad del cohete en función del tiempo. (b) ¿Cuándo es cero la velocidad?

El tiempo que le tomara a la velocidad llegar a cero es de diez segundos.
- Un huevo cae desde una ventana del segundo piso, tarda 1.10 s en caer y alcanza 13.0 m/s justo antes de golpear el suelo. Al contacto, el huevo se detiene completamente en 0.135 s. Calcule las magnitudes medias de su aceleración al caer y al detenerse.
Para este problema Podemos usar la ecuación 9 de “movimientos en 1-D” y resolver la ecuación por la aceleración que nos proporciona la ecuación para aceleración promedio. Asumiendo que cuando calculamos la aceleración al caer, el objeto empieza en reposo, por lo que su velocidad inicial es cero y cuando el huevo se detiene su velocidad inicial es la velocidad mientras cae. Esto es debido que, aunque es el mismo objeto los momentos en que estamos haciendo los cálculos no son los mismos por lo tanto los parámetros varían.
Cuando el huevo cae.Cuando el huevo
se detiene.
- El primer automóvil supersónico del mundo, acelera desde el reposo a 1750 km/h en 12 s. cuál es su aceleración?
- Un cohete se eleva con aceleración constante a una altitud de 65 km, en cuyo punto su velocidad es de 3.4 km/s. (a) ¿Cuál es su aceleración? (b) ¿Cuánto tiempo dura el ascenso?
El
cohete dura 38 segundos en alcanzar una altura de 65 km con una aceleración de 0.089
m/s2.
- Un automóvil que se mueve inicialmente a 50 mi/h comienza a disminuir a una velocidad constante a 150 pies antes de un semáforo. Si el automóvil se detiene por completo justo en el semáforo, ¿cuál es la magnitud de su aceleración?
Como este problema no depende del tiempo podemos usar la misma ecuación que
usamos en el problema anterior para resolver la aceleración. Su velocidad
inicial es dada en el problema y exige que su velocidad final sea cero, también
que su desplazamiento es de 150 pies. Es decir, x – x0 = 150 pies. Como
las unidades de medida entre la distancia y la velocidad son diferentes debemos
convertirlas para que concuerden. Para variar decidí usar ft/s (pies por
segundo) para definir la velocidad.
El automóvil experimenta una aceleración de -17.8 ft/s2 hasta hacer su parada completa. Su aceleración es negativa pues esta es en dirección contraria al desplazamiento, produciendo que el automóvil pierda velocidad.
- Dejas caer una piedra en un pozo profundo y 2.4 s después de escuchar un chapoteo. ¿A qué profundidad está el agua? Desprecie el tiempo de viaje del sonido.
Este problema
Podemos resolverlo asumiendo algunas condiciones iniciales que serán útiles para
utilizar la ecuación 13. El desplazamiento es hacia abajo lo que significa que
la aceleración es debido a la gravedad por lo que a = g; como dejamos caer la
roca podemos decir que su velocidad y posición inicial son cero. Si asumimos
que el eje de coordenadas es y podemos decir que es positivo hacia arriba y
negativo hacia abajo por lo que la gravedad será negativa y nuestro desplazamiento
también. Podemos elegir qué hacia abajo es positivo y hacia arriba es negativo
haciendo la gravedad y nuestro resultado positivos, en este caso la magnitud no
cambia y la elección es completamente arbitraria. Yo decidí que sea positivo
hacia abajo pues prefiero trabajar con números positivos, pero pueden elegir
otro si lo desean.
El pozo tiene una profundidad de 28 metros según nuestro análisis.
- Un modelo de cohete abandona el suelo y se dirige directamente hacia arriba a 73 m/s. (a) ¿Cuál es su altitud máxima? Encuentre su rapidez y altitud en (b) 1.2 s, (c) 3 s y (d) 6.7 s.
Como la parte (a) de este problema no depende del tiempo podemos usar la misma ecuación que usamos en el problema anterior para resolver la aceleración pero esta vez para encontrar la altitud máxima. Recordemos que a máxima altitud v = 0. Usaremos el eje y positivo hacia arriba y negativo hacia abajo así que a = -g y la posición inicial es el suelo x0 = 0.
Para encontrar la
rapidez y altitud a diferentes tiempos usamos la ecuación 9. Recordemos que la
rapidez es otra forma de llamar la velocidad.
(b) 1.2 s
(c) 3 s
(d) 6.7 s
Mientras más pasa
el tiempo más se acerca el cohete a su altura máxima por lo que su velocidad
disminuye.
- La posición de un objeto en función del tiempo t viene dada por x = bt4, con b una constante. Encuentre una expresión para la velocidad instantánea y demuestre que la velocidad promedio en el intervalo desde t = 0 hasta cualquier momento t es un cuarto de la velocidad instantánea en t.
Podemos encontrar la velocidad instantánea tomando
la derivada mientras que la velocidad promedio la determinamos usando la ecuación
2 de “movimientos en 1-D”.
Para la velocidad instantánea.
Para la velocidad promedio.
Si tomamos la proporción de estas dos entidades
(dividimos una por la otra) tenemos.
Movimientos en dos o mas dimensiones.
- Camina al oeste 250 m, luego al norte 142 m. ¿Cuáles son la magnitud y la dirección de su vector de desplazamiento?
Aquí tenemos los componentes en direcciones cardinales. Si usamos el
plano cartesiano de forma ordinaria podemos decir que el oeste está en la dirección negativa del eje x y el norte está en la dirección positiva del eje
y. para encontrar su magnitud y dirección usamos las siguientes ecuaciones.
El objeto se
mueve 288 m con una inclinación de -29.6 grados.
- Un objeto se mueve a 21 m/s a 165 grados en sentido antihorario desde el eje x. Encuentra las componentes x e y de su velocidad.
Aquí tenemos
la magnitud y la dirección y deseamos encontrar los componentes del eje x e y
- Desea remar directamente a través de un río de 59 m de ancho. Puede remar a una velocidad constante de 1,7 m/s en relación con el agua, y el río fluye a 0,75 m/s. (a) ¿Qué dirección debe tomar? (b) ¿Cuánto tiempo te tomará cruzar el río?
Este es un
ejemplo de movimiento relativo así que debemos analizar la información proporcionada
para ver que tenemos. Primero vemos
la velocidad del bote con respecto al agua. Esta nos fue dada en su magnitud y
no sus componentes de vector que podemos definir como v’; luego la velocidad
del río, V. Si hacemos una gráfica tendremos.
Agregando un
sistema de coordenadas tenemos que x es en dirección con el río e y es en dirección que él cruza el bote (esto es completamente arbitrario pueden elegir un orden
diferente). Como tenemos la magnitud de la velocidad del bote debemos encontrar
su velocidad con respecto a y pero para ello necesitamos encontrar el ángulo. Usando
trigonometría podemos encontrar el ángulo al igual que usando la ecuación para
la velocidad relativa.
La dirección que
debe tomar al remar es de 26 grados con y tardará 38.6 segundos en cruzar. La velocidad
que experimenta será de 1.53 m/s mientras que con respecto al suelo será de
2.28 m/s.
- Un carpintero lanza una teja horizontalmente desde un techo de 8 m de altura a 15 m/s. (a) ¿Cuánto tiempo tarda la teja en llegar al suelo? (b) ¿Qué tan lejos se mueve horizontalmente?
Este problema
es similar al ejemplo del vehículo que salto. Tenemos la altura y0 =
8m y su velocidad en el eje x v0x = 15 m/s. el tiempo puede ser
calculado usando la ecuación 10 de “movimientos
en dos o mas dimensiones”
Como solo existe aceleración
en y debido a la gravedad, ax = 0 y la posición inicial de x también
es cero.
La teja viaja unos 19.5 m y tarda 1.3 s en tocar el suelo.
- Estima la aceleración de la Luna, que completa una órbita casi circular de 385,000 km de radio en 27 días.
Si usamos
la ecuación para encontrar el periodo y la resolvemos por la aceleración entonces
podremos resolver este problema
Ahora debemos
convertir las unidades en números vayan acorde al sistema de unidades.
Como Pudieron notar la mayoría de los pasos algebraicos fueron omitidos pues son muy obvios pero les deje suficiente pistas para que puedan hacer las derivaciones ustedes mismos. Con esto estamos al dia con respecto al contenido del movimiento en múltiples dimensiones. Ya para la próxima publicación hablaremos de la fuerza primera desde un punto de vista teórico y luego matemático. Así mismo comenzaré con una serie nueva de publicación en las cuales hablaré de temas de importancia en la física. No olviden dejar sus comentarios y sugerencias. si conocen un método mejor para hacer estos ejercicios por favor de compartir y si les interesa algo en particular por favor de compartir.









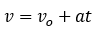

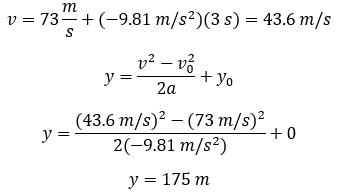

















Comentarios
Publicar un comentario