Movimiento Circular y Fuerza de Torsion
Movimiento
circular
El
movimiento de rotación se refiere a cualquier cosa que gire o se mueva en una
trayectoria circular. También se le llama movimiento angular o movimiento
circular. Debido a que el movimiento de rotación se define como un movimiento
circular alrededor de un eje central, es uno de los movimientos más comunes en
el universo. Desde el movimiento planetario hasta un disco DVD, desde una hoja
de sierra hasta moléculas, todos giran. La rotación es en cierto modo similar a
un desplazamiento 1D, así que usemos esto para encontrar ecuaciones
analógicas que puedan relacionar ambos.
Comencemos
con la definición de revoluciones, que es una rotación completa
alrededor de un eje, el objeto comienza y termina en la misma posición. La
distancia desde el eje de rotación hasta la trayectoria del objeto se fija
regularmente (es la misma para toda la rotación) y se denomina radio
indicado por la letra r. El movimiento circular se mide en grados o
radianes con una revolución igual a 360◦
o 2π
radianes, aunque el radián es una unidad adimensional. El
desplazamiento de una revolución se llama circunferencia y se denota con
la letra C. Mientras medimos la distancia que ha recorrido el objeto, un
segmento de la circunferencia es un arco que se denota con la letra s.
Una circunferencia está determinada por.
C=
2πr
Ahora,
la velocidad a la que gira un cuerpo es su velocidad angular. Una unidad
muy conocida para esto es el rpm (revolución por minuto) pero también
podríamos expresarlo como revoluciones por segundo (rev/s) o radianes
por segundo (rad/s o simplemente s-1 recordando que 1
rev = 2π rad). Una vez más, tomamos una letra griega para definir la
velocidad de rotación ω.
Ya
dijimos que θ es el desplazamiento angular y t es el tiempo
mientras que ∆ se usa comúnmente para definir la diferencia (entre la
posición final y la posición inicial o dos puntos arbitrarios). Cuando la
velocidad angular está cambiando, definimos el límite sobre un intervalo
arbitrariamente corto como la velocidad angular instantánea.
Ejemplo
Un
aerogenerador gira a 21 rpm. Expréselo en rad/s.
Velocidad Angular y Lineal
Los
puntos individuales en un objeto giratorio también experimentan velocidad lineal,
utilizando la definición de desplazamiento circular podemos establecer una
relación entre la velocidad lineal y angular.
Debido
a que el radio r es constante y s es la longitud del arco (la
distancia real recorrida por un punto en un objeto giratorio), el término ds/dt
es solo la velocidad lineal v, entonces
Por
lo tanto, la velocidad lineal de cualquier punto de un objeto giratorio es
proporcional tanto a la velocidad angular como a la distancia desde ese punto
hasta los ejes de rotación. Indicación de que en un objeto giratorio todos los
puntos experimentan la misma velocidad angular pero no necesariamente la misma
velocidad lineal.
Aceleración
angular
Si
la velocidad angular cambia, entonces el objeto sufre una aceleración angular
α. Tomando el límite se obtiene una aceleración angular instantánea. Si no
tomamos el límite, entonces tenemos la aceleración promedio. Ya hemos visto
esto antes con términos lineales.
Su
sentido será horario o antihorario dependiendo de si la aceleración se produce
en el mismo sentido o en sentido contrario a la velocidad angular (un objeto se
acelera o se frena). Algunas de las unidades más comunes son rad/s2,
rpm/s o rev/s. La aceleración angular también se puede reescribir
en términos de movimiento lineal.
Esta
aceleración lineal se llama aceleración tangencial. Ya sea que haya o no
aceleración angular, los puntos en un objeto giratorio experimentarán una
aceleración radial porque están en movimiento circular (la aceleración es la
segunda derivada de la posición, por lo tanto, siempre que haya un cambio en la
posición, habrá una aceleración). la aceleración radial viene dada por ar =
v2/r. Usando nuestra ecuación # podemos reescribir la
aceleración radial en términos de rotación.
Debido
a que definimos estas ecuaciones de manera análoga a sus partes lineales, las
relaciones entre la posición lineal, la velocidad y la aceleración también se
aplican a la posición angular, la velocidad y la aceleración, y si la
aceleración angular es constante, las ecuaciones de movimiento también se
pueden usar cuando hacemos la sustitución correspondiente.
Ejemplos
Durante
el arranque, la turbina de una central eléctrica acelera desde el reposo a 0,52
rad/s2. (a) ¿cuánto tiempo le toma alcanzar su velocidad de operación de 3600
rpm? (b) ¿cuántas revoluciones hace durante este tiempo?
De
la misma manera que recolectamos información para resolver problemas lineales,
lo haremos en este caso y luego veremos qué ecuación de movimiento nos es más
favorable.
(a)
El
problema nos dice que la turbina parte del reposo con una posición angular de θ0
= 0, ω0 = 0 y α= 0.52. y queremos saber el tiempo que tarda en
alcanzar una velocidad de 3600 rpm. Para este caso podemos usar nuestra
segunda ecuación de movimiento y resolverla para el tiempo.
La
velocidad que nos dan es la diferencia ∆ω, ahora debemos convertirla
para usarla en nuestra ecuación.
(b)
Para
determinar el número de revoluciones que realiza durante este tiempo
utilizaremos la ecuación 4.
Un
tiovivo parte del reposo y acelera con una aceleración angular de 0.010
rad/s2 durante 14 s. (a) ¿Cuántas revoluciones hace
durante este tiempo? (b) ¿cuál es su rapidez angular promedio?
(a)
Hacemos lo mismo que en el problema anterior. Partimos del reposo y
experimentamos una aceleración angular α durante 14 segundos. El
número de revoluciones se puede calcular como en el problema anterior.
(b)
para calcular la velocidad angular promedio, usamos la definición de velocidad
angular para ello.
La
velocidad angular final es el doble de la velocidad media. Esto es de esperar
porque comenzamos desde velocidad cero y aceleramos a una velocidad constante,
por lo que la velocidad promedio se alcanza a la mitad del período de
aceleración, momento en el cual el objeto en cuestión gira a la mitad de la
velocidad angular.
Torque
o Esfuerzo de Torsión
La
segunda ley de Newton (F = ma) se aplica a todo movimiento, pero su
aplicación puede ser engorrosa según el movimiento del objeto (como los objetos
giratorios), por lo tanto, intentemos recrear un enfoque análogo que se pueda
aplicar a las cantidades rotacionales. Para hacer esto necesitamos análogos
rotacionales de fuerza, masa y aceleración. Afortunadamente para nosotros, ya
encontramos un análogo de la aceleración de rotación, ahora busquemos algo para
la fuerza.
Uno
de los casos en los que vemos rotacional en nuestra vida diaria viene en forma
de desenroscar un perno de tuerca. Para esto normalmente usamos una llave o una
llave ajustable (que es una llave para varios tamaños). Dependiendo de qué tan
larga sea nuestra llave inglesa y dónde o cómo la sostengamos, la tarea puede
parecer simple o muy problemática (si tiene la experiencia de cambiar una
llanta ponchada, lo sabe muy bien). Tanto la distancia desde el eje de rotación
como la posición de nuestras manos tienen un gran impacto en cómo la fuerza
aplicada interactuará al aflojar o apretar una tuerca, al igual que en un
balancín entre un adulto y un niño, la distancia entre el punto de pivote para
el niño y el adulto determinarán la posición de equilibrio. En este caso, la
eficacia de la fuerza para provocar cambios en un movimiento de rotación
depende de la distancia desde el eje de rotación y la magnitud de la fuerza.
La
efectividad de la fuerza también depende de la dirección en la que se aplica,
de hecho, la fuerza es más efectiva cuando es perpendicular a la distancia con
respecto al eje de rotación. Con base en estas consideraciones, definimos el
torque como el producto de la distancia r desde el eje de rotación y la
componente de la fuerza F perpendicular a ese eje. Usamos la letra
griega τ para indicar torque.
El
ángulo θ se forma entre el vector de fuerza y el vector de distancia,
debido a esto cuando r // F el ángulo es 0° o 180° y no
hay torsión. Cuando la fuerza se aplica en un ángulo que es perpendicular a r,
se crea un brazo nivelado que es la distancia efectiva a la que actúa F.
Lo llamamos efectivo porque es donde el torque es mayor.
El
torque como una fuerza de torsión en el análogo de rotación de la segunda ley
de Newton. La unidad de medida es el newton-metro, que es la misma unidad que
la energía, pero es una cantidad física diferente, por lo que reservamos Joule
solo para la energía.
Se
necesita un par de torsión de 103 N.m para iniciar la rotación de una
puerta giratoria. Si un niño puede empujar con una fuerza máxima de 95 N,
¿a qué distancia del eje de rotación de la puerta debe aplicar esta fuerza?
Como
este problema nos dice que la fuerza de empuje que ejerce el niño es una fuerza
máxima, el ángulo en el que se aplica esta fuerza es de 90°. Ahora vamos
a resolver la ecuación para la distancia.
Un
ratón de 55 g corre hacia el final de la manecilla de minutos de 17
cm de largo de un reloj de pie cuando el reloj marca 10 después de
la hora. ¿Qué torsión ejerce el peso del ratón sobre el eje de rotación de la
manecilla del reloj?
La
solución a este problema requiere el uso de conocimientos comunes relacionados
con la descripción del problema. Primero, convierta todas las unidades al
estándar SI.
- m
= 55 g à
0,055 kg
- r
= 17 cm à
0,17 m
como
un reloj da una vuelta completa después de 60 minutos, podemos dividir 360°
entre 60 y obtenemos que el minutero se mueve 6° por minuto.
Debido a que la manecilla está 10 minutos después de la hora, obtenemos 60°
o π/3 radianes, por lo que el ángulo entre la fuerza y el vector de
posición radial desde el eje de rotación hasta el punto donde se aplica la
fuerza es de 120°.
Nuestra
fórmula para el Torque es
Podemos
aplicar la segunda ley de Newton al ratón para encontrar la magnitud de la
fuerza.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/JMDFisica
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre las matemáticas.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Blogger: aprendematematicasjmd.blogspot.com






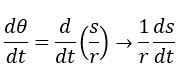


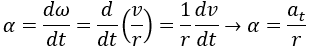

















Comentarios
Publicar un comentario