Colisiones
En física, cualquier evento en el que dos o más cuerpos ejercen fuerzas entre sí se denomina colisión. Algunos ejemplos son bolas en una mesa de billar golpeándose entre sí, una pelota de tenis golpeando una raqueta, una pelota de béisbol y un bate, un asteroide y un planeta, e incluso las galaxias pueden chocar entre sí, de hecho, se espera que en 5 mil millones de años la galaxia de Andrómeda chocará con la vía láctea. Todas estas colisiones deben cumplir con dos criterios importantes; deben ser breves, durar poco tiempo en el contexto general del movimiento del objeto que choca. En segundo lugar, las colisiones deben ser intensas. Las fuerzas entre los objetos que interactúan son mucho mayores que cualquier fuerza externa que pueda estar actuando sobre el sistema. Para ver estos criterios en funcionamiento, examinemos el caso de las bolas de una mesa de billar que chocan con otras. El tiempo de colisión es corto en comparación con el tiempo que tardan las bolas en rodar sobre la mesa, y las fuerzas internas son mucho más fuertes que cualquier fuerza externa y determinan el movimiento de las bolas después de la colisión.
Impulso
Debido a que las
fuerzas que pueden alterar el impulso de los objetos que chocan son internas al
sistema, la segunda ley de Newton dice:
(1)
Donde F es
la fuerza promedio que actúa sobre un objeto durante una colisión que dura un tiempo
∆t. El producto de la fuerza promedio y el tiempo se llama impulso.
Está dado por el símbolo J. un impulso dado da como resultado un cambio
igual en el momento, por lo que algunas personas definen el impulso y el
momento como lo mismo.
Un impulso J
produce la misma cantidad de cambio sin importar si involucra una fuerza grande
durante un tiempo más corto o una fuerza más pequeña durante un tiempo más
largo. Debido a que la fuerza en una colisión fluctúa vívidamente, encontramos
el impulso integrando la fuerza con el tiempo.
(2)
- Ejemplo 1. Dos satélites de 140 kg chocan a una altitud
donde g = 8.7 m/s2 y la colisión imparte un impulso de 1.8
× 105 N∙s a cada uno. Si la colisión dura 120 ms, compare el impulso
de colisión con el impartido por la gravedad. Tu resultado debería mostrar por
qué puedes despreciar la fuerza externa de la gravedad.
Podemos usar la ecuación 1 para
calcular el impulso impartido por la gravedad en un solo satélite. Como no
conocemos la fuerza, debemos calcularla usando la segunda ley de Newton.
Masa = 140 kg
Aceleración = g = 8.7
m/s2
Tiempo = 120 msec
= 0.12 s
Si comparamos este valor con el impulso
impartido por la colisión, encontramos que
El impulso impartido
por la gravedad es muy pequeño por lo que se puede despreciar.
Aunque introdujimos
el impulso en el contexto de la colisión, son útiles en situaciones en las que
se aplica una fuerza intensa durante períodos cortos de tiempo, por ejemplo,
motores de cohetes pequeños.
- Ejemplo 2. Estás trabajando en el control de la misión de una
sonda espacial interplanetaria. Una corrección de trayectoria exige el disparo
de un cohete que imparte un impulso de 5.64 N∙s. Si el empuje promedio
del cohete es de 135 mN, ¿Cuánto tiempo debe disparar el cohete?
En este caso, estamos resolviendo para el
tiempo, por lo que necesitamos manipular nuestra ecuación y resolver para
encontrar el tiempo.
El cohete debe
dispararse durante un mínimo de 41,8 segundos para tener éxito en la
corrección de la trayectoria.
Ahora, en una
colisión, la energía cinética puede o no conservarse. Esto se debe a las
fuerzas que actúan durante la colisión. Si la energía se conserva, la colisión
se considera elástica, si no, la llamamos inelástica.
Una colisión elástica
requiere que las fuerzas entre los objetos que chocan sean conservativas, luego
la energía cinética se transforma en potencial y se libera cuando termina la
colisión. Ejemplos de colisiones elásticas pueden ser una pelota de baloncesto
que rebota en el tablero o dos imanes que se acercan con sus polos norte
enfrentados; se repelen y cambian de dirección sin tocarse. Las interacciones
en el nivel atómico son a menudo elásticas, mientras que en el ámbito
macroscópico, las fuerzas no conservativas producen calor o deforman
permanentemente los objetos que chocan, privándolos de energía cinética.
Algunos ejemplos que podemos usar son la colisión entre un automóvil
estacionado y un camión, ya que los dos se deslizan juntos y el metal arrugado
se entrelaza, o una bola de nieve que golpea contra un árbol, estos son buenos
ejemplos de colisiones inelásticas.
Colisiones
inelásticas
En una colisión totalmente inelástica, los
objetos que chocan se unen para formar un solo objeto. Implica la máxima
pérdida de energía consistente con la conservación del momento, por lo tanto,
el movimiento está determinado completamente por la conservación del momento,
lo que facilita su análisis.
Considere dos masas m1 y
m2 con velocidades iniciales v1 y v2
que experimentan una colisión totalmente inelástica. Después de la colisión, se
unen para formar un solo objeto de masa m1 + m2 y
velocidad final vf. La conservación de la cantidad de
movimiento establece que la cantidad de movimiento inicial y final deben ser
iguales (recuerde que las velocidades y la cantidad de movimiento son vectores
y deben considerarse para casos de múltiples dimensiones).
(3)
Dadas cuatro de las
cinco cantidades, podemos resolver para la quinta.
- Ejemplo 3. El capitán de hockey decide medir la velocidad del disco. Carga un cofre pequeño de espuma de poliestireno con arena, dando una masa total de 6.4 kg. Lo coloca en reposo sobre hielo sin fricción. El disco de 160 g golpea el cofre y se incrusta en la espuma de poliestireno. El cofre se mueve a 1.2 m/s ¿Cuál fue la velocidad del disco?
Este
es un buen ejemplo de una colisión inelástica ya que el disco se incrustará en
el cofre de espuma de poliestireno y se convertirá en uno. Llamemos a la masa
del cofre de espuma de poliestireno m1 y a la masa del disco m2.
Dado que el cofre de espuma de poliestireno está en reposo, su velocidad es
cero, pero después de la colisión, la velocidad final es de 1.2 m/s.
Ahora podemos analizar la ley de conservación de la cantidad de movimiento y
ver cómo se desarrolla.
- Ejemplo 4. El péndulo balístico mide la velocidad de objetos que se mueven rápidamente como balas. Consiste en un bloque de madera de masa M suspendido de cuerdas verticales (ver imagen a continuación). Una bala de masa m golpea y se incrusta en el bloque, y el bloque se balancea hacia arriba a lo largo de una distancia vertical h. Encuentra una expresión para la velocidad de la bala.
Al analizar la declaración, podemos notar que suceden
dos eventos: la bala que golpea el bloque y la elevación del bloque. En el
primer caso tenemos una típica colisión inelástica donde los dos objetos chocan
y se convierten en uno nuevo. Aquí se conserva la cantidad de movimiento, pero
no la energía, mientras que en el segundo caso el bloque sube y ahora una
fuerza externa neta (de la tensión de la cuerda y la gravedad) actúa para
cambiar la cantidad de movimiento. Como la gravedad es conservativa y la
tensión de la cuerda no realiza trabajo, la energía mecánica se conserva. En términos matemáticos podemos expresarlo de la siguiente
manera.
Como el bloque no se mueve inicialmente, su velocidad es cero. Cuando el impulso del bloque que gira hacia arriba ya no se conserva, pero sí su energía, entonces hacemos el análisis de conservación de energía K0 + U0 = Kf + Uf. El potencial inicial es cero y toda la energía se convierte en movimiento y el potencial final viene dado por (m + M)gh y la energía cinética es cero en la altura máxima (si no entiendes de dónde vienen estas asunciones entonces debes analizar el estado inicial y final del problema).
Podemos tomar la primera ecuación y resolverla para la velocidad final.
Esta la Podemos sustituir en la ecuación de la energía
y resolverla para encontrar una expresión para la velocidad de la bala.
Cuanto menor sea la masa de la bala, mayor debe ser la velocidad para llevar un impulso dado; eso se refleja en el factor m solo en el denominador. Cuanto mayor sea el aumento h, obviamente, mayor será la velocidad de la bala. Pero la velocidad escala no como h en sí misma, sino como √h. Eso se debe a que la energía cinética, que se convirtió en energía potencial del aumento, depende de la velocidad al cuadrado.
- Ejemplo 5. En una colisión totalmente inelástica entre dos masas iguales, con una inicialmente en reposo, demuestre que se pierde la mitad de la energía cinética inicial.
Dado
que se trata de una colisión inelástica, podemos hacer un análisis de su
momento.
Resolviendo para la velocidad final obtenemos.
Como estamos interesados en el cambio de energía cinética, observamos la diferencia entre la energía cinética antes y después de la colisión.
Ahora las masas son las mismas (m1 = m2 = m) y una de las masas está inicialmente en reposo, elegí m2 para que esté en reposo, lo que hace que v2 = 0. Y la velocidad de m1 es solo v para que podamos simplificar la ecuación.
Vemos
que se perdió la mitad de la energía cinética y que ∆K es negativo indicando
que la energía cinética inicial fue mayor que la final.
Colisiones
elásticas
Entonces, a estas alturas sabemos que la cantidad de momento se conserva para casi cualquier colisión. En una colisión elástica también se conserva la energía cinética. El caso más general ofrece dos objetos de masas m1 y m2 con velocidades iniciales v1i y v2i chocan y experimentan velocidades finales v1f y v2f. sus declaraciones de conservación se convierten.
y
Dadas las velocidades iniciales, nos gustaría predecir el resultado de una colisión. En el caso inelástico, teníamos suficiente información para resolver el problema incluso para casos bidimensionales, pero para colisiones elásticas, el caso bidimensional nos deja con cuatro incógnitas y solo tres ecuaciones para trabajar con los componentes de conservación del momento y ecuaciones escalares individuales para conservación de energía. esta no es suficiente información para obtener una solución general (se puede encontrar más de esto en un tema más profundo de cálculo multivariable). Por lo tanto, debemos examinar primero las colisiones elásticas unidimensionales y ver qué podemos aprender de allí que sea aplicable al caso bidimensional.
Colisiones
elásticas en una dimensión
dos objetos chocan de frente, su estructura interna es insignificante, por lo que simplemente podemos suponer que el tamaño y la forma de los objetos no importan. Las fuerzas internas actúan a lo largo de la misma línea que el movimiento. En un caso unidimensional, la ecuación de conservación del momento y energía cinética tiene solo un componente no trivial.
y
Juntando términos semejantes podemos simplificar nuestras ecuaciones.
En la ecuación de la energía cinética, las mitades se anulan entre sí. Podemos reescribir esos términos como la diferencia de cuadrados a2 - b2 = (a + b) (a - b).
Dividiendo estas dos ecuaciones podemos cancelar algunos términos.
(4)
Reorganizando una vez más.
(5)
Esta
ecuación nos dice que las velocidades relativas permanecen sin cambios después
de la colisión, aunque su dirección se invierte (si dos objetos chocan a 5
m/s se separan a - 5 m/s).
Ahora
podemos resolver para las velocidades finales.
(6)
Resolviendo para v1f.
(7)
De
manera similar, si sustituimos v1f y resolvemos para v2f
obtenemos.
(8)
Ahora
podemos aplicar condiciones iniciales e imaginar tres casos especiales para
simplificar el problema:
Si
m2 está inicialmente en reposo, entonces v2i =
0 y
Caso
1: m1 << m2
En
este caso debemos analizar el término fraccionario para las masas.
Entonces la ecuación se reduce a
(9)
Caso 2: m1
= m2
(10)
Caso 3: m1 >> m2
(11)
(12)
- Ejemplo 6. Jugando en la calle, un niño lanza accidentalmente una pelota a 18 m/s hacia el frente de un automóvil que se mueve hacia él a 14 m/s. ¿Cuál es la velocidad de la pelota después de que rebota elásticamente del auto?
Como se trata de un problema de colisión elástica, se
conservan tanto la energía mecánica como el momento lineal. Elegí llamar a la
pelota masa m1 y al carro masa m2, y sus velocidades v1i
para la rapidez inicial de la pelota y v1f para la rapidez
final de la pelota y v2i y v2f para la
rapidez inicial y final del carro respectivamente.
Podemos usar manipulación algebraica para encontrar
una ecuación para las velocidades finales o podemos usar las ecuaciones que
encontramos antes para suposiciones generales.
Suponiendo
v+ en la dirección del movimiento del automóvil y m1
<< m2, las ecuaciones se convierten en
Dado
que el automóvil es más masivo que la pelota, no esperamos que cambie su
velocidad o dirección, sin embargo, esperábamos que la pelota cambiara de
dirección y tuviera un cambio en su velocidad.
El análisis de colisión elástica, especialmente el de dos dimensiones, se usa en el análisis de parámetros de impacto que se usa comúnmente en programas de investigación de la escena del crimen para determinar la trayectoria de una bala o el punto de vista del tirador a partir de los patrones de salpicaduras de sangre.
- Ejemplo 7. Una pelota de croquet golpea una pelota estacionaria de igual masa. El choque es elástico y la bola incidente sale disparada a 30° de su dirección original. ¿En qué dirección se mueve la otra bola?
La visualización de este problema es de gran ayuda
para entender qué está pasando y cómo abordarlo. Dado que el problema solo
pregunta por la dirección, las magnitudes de las velocidades no importarán.
Usando nuestras ecuaciones para momento y energía, nuestras masas se cancelarán
ya que son todas iguales. Y las ecuaciones se reducirán solo a términos de
velocidad.
Ahora podríamos escribir la ecuación en dos
componentes, pero dado que tenemos algunos términos elevados al cuadrado, esto
puede complicar un poco más las cosas. Afortunadamente, podemos representarlo
usando el producto escalar y usar sus propiedades en su lugar.
Recuerda que el producto escalar de dos vectores es el
producto de sus magnitudes por el coseno del ángulo entre ellos A∙B = AB cosθ. El ángulo
entre un vector y sí mismo es cero, el producto escalar es simplemente A∙A =
A2 cos (0) = A2.
Porque el ángulo entre v1f y v2f
es igual a θ + 30°. Si tomamos la
ecuación de la energía y la reescribimos, obtenemos
Entonces,
podemos reorganizar
También
podríamos simplemente haberle restado la ecuación de energía. Como ninguna de
las velocidades es cero, debemos hacer que el coseno sea cero. Resulta que el
coseno es cero a 90°. Así θ + 30° = 90° lo que implica
que θ = 60°.
La
colisión bidimensional también debe conservar la cantidad de movimiento total
antes y después de la colisión, por lo tanto, tanto la cantidad de movimiento
inicial como la final forman pares de vectores de igual magnitud y direcciones
opuestas. En las colisiones elásticas, la conservación de la energía requiere
que los momentos tengan los mismos valores. La física de alta energía hace uso
de esto al transformar el marco del centro de masa y los vectores de momento y
velocidad resultantes y luego devolverlos al marco de laboratorio original para
comprender las fuerzas fundamentales entre las partículas elementales.
Aunque en estos ejemplos no utilizamos cálculos de vectores, debemos recordar que la fuerza, y la velocidad son magnitudes vectoriales. Lo más importante por ahora es entender los conceptos básicos de las colisiones. Cuando revisitemos el tema entonces iremos más profundo en el aspecto matemático.
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/JMDFisica
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
También pueden seguir nuestro otro blog si les
interesa aprender sobre las matemáticas.
- Facebook: https://www.facebook.com/AprendeMatematicasJMD
- Blogger: aprendematematicasjmd.blogspot.com











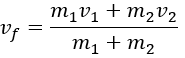









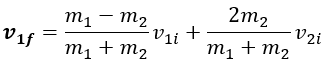
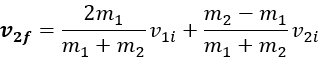








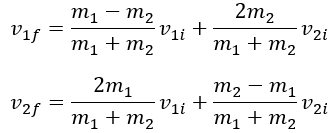








Comentarios
Publicar un comentario