Sistemas de Muchas Partículas
En
publicaciones anteriores hablamos sobre cómo la fuerza y el trabajo afectan a
un objeto, pero ahora veremos cómo los objetos interactúan entre sí y cómo las
propiedades estudiadas anteriormente se ven afectadas por esto.
Un sistema de partículas significa un grupo de partículas interrelacionadas. La teoría de muchas partículas proporciona la base para comprender el comportamiento macroscópico de vastos conjuntos de partículas que interactúan entre sí. Uno de los problemas más comunes estudiados por esta teoría son los cuerpos rígidos, pero para poder trabajar en este problema primero debemos entender el fundamento sobre el cual se construye esta teoría de muchas partículas. Para lograr esto, discutiremos la idea de centro de masa, momento lineal y colisiones. Esta es solo una introducción al sistema de partículas y usaremos algunos conceptos de cálculo para derivar algunas de las ecuaciones.
Centro de masa
Considere un sistema de muchas partículas. Si aplicamos la segunda ley de Newton a la i-ésima partícula del sistema, tenemos.
PODEMOS HACER
ESTO PORQUE ES BÁSICAMENTE SIMPLEMENTE MULTIPLICAR POR 1 YA QUE M/M =
1.
(1)
El centro de masa es una posición promedio
de todas las masas involucradas en una configuración específica. Es como esta
posición donde todas las masas están equilibradas y la fuerza neta es cero. Veamos
algunos ejemplos.
Ejemplo 1. Centro
de masa de pesas
Todavía tenemos que definir la posición de las masas. Para continuar necesitamos aplicar un sistema de coordenadas. Como siempre, las elecciones de coordenadas son arbitrarias, por lo que la elección que hagamos puede simplificar o hacer que sea más difícil de resolver, pero la respuesta que obtengamos será válida para la elección que hagamos. Lo que haré es elegir x = 0 en dos posiciones diferentes; primero en m1 y x+ a la derecha, y luego en m2 y x+ a la izquierda y ver qué valor obtenemos para nuestro centro de masa.
- x = 0 at m2 y x+ a la izquierda.
El
centro de masa se encuentra a 0.66m a la izquierda de m2.
Si
notamos que las dos cantidades sumadas dan la longitud total e
independientemente de la elección del sistema de coordenadas, el punto donde se
supone que está el centro de masa es el mismo (básicamente, no importa desde
dónde lo midamos, estará siempre en el mismo lugar).
Ejemplo 2. Centro de masa en un plano 2D
El
arreglo es un triángulo equilátero de longitud L. si las tres masas son
iguales, el centro de masa es equidistante de todas las masas, pero si
tuviéramos que elegir m1 = m3 y m2 =
2m1, el centro cambiará porque la distribución de masa cambió.
- Para las tres masas iguales entre sí (m1 = m2 = m3) y un sistema de coordenadas centrado en m2 podemos extrapolar la siguiente información.
Como
el triángulo es un triángulo equilátero, todos los ángulos internos miden 60
grados. Elegí un sistema de coordenadas centrado en m2
con x+ a la derecha e y+ hacia abajo. La posición de m2
es el origen (x2=0, y2=0). La altura de las
masas m1 y m3 es la misma y usando las
propiedades del coseno podemos encontrar la altura del triángulo que también es
igual al valor de y1 e y3.
El
centro de masa con respecto a x.
Como
el triángulo es equilátero, la distancia x3 y x1
tienen el mismo valor absoluto, por lo tanto, xCM = 0.
El
centro de masa con respecto a y.
Las
coordenadas para el centro de masa son (0, 0.58L).
- Si m1 = m3 y m2 = 2m1, ¿Cuál será el centro de masa?
Elegí
el mismo sistema de coordenadas y simplemente cambié las masas en la ecuación.
Con respecto a x.
Con respecto a y.
Las coordenadas
para el centro de masa son (0, 0.43L).
La materia como fuente continua
 |
| Una hoja de metal es un excelente ejemplo de materia continua |
Hasta
ahora hemos estudiado la materia como un punto en el espacio, pero sabemos que
está compuesta de partículas individuales, y calcular el centro de masa de cada
partícula individual puede ser una tarea bastante tediosa, por lo que la
consideramos como una distribución continua. Al considerar la materia continua
como compuesta de piezas individuales de masa ∆mi, con
vectores de posición ri, llamamos a estas piezas elementos de masa. El centro de masa de todo
el trozo está dado por . En el límite, a medida que el elemento de masa se vuelve
arbitrariamente pequeño, esta expresión se convierte en una integral.
Discutiremos
la idea más profundamente cuando la revisemos en el futuro.
Momento
lineal
Esta última forma
se parece a la fórmula para el centro de masa, por lo que podemos multiplicar y
dividir por la masa total del sistema M.
 es la velocidad
del centro de masa. ¿Qué significa esto? La expresión es similar al momento de
una partícula individual. No necesitamos conocer cada movimiento en un cuerpo
complejo, solamente su centro es suficiente como el caso del vehículo que choca
con el árbol no necesitamos calcular el movimiento de cada hoja o el movimiento
de cada tornillo en el vehículo al momento de impacto podemos simplificar el
problema usando sus centros de masa.
es la velocidad
del centro de masa. ¿Qué significa esto? La expresión es similar al momento de
una partícula individual. No necesitamos conocer cada movimiento en un cuerpo
complejo, solamente su centro es suficiente como el caso del vehículo que choca
con el árbol no necesitamos calcular el movimiento de cada hoja o el movimiento
de cada tornillo en el vehículo al momento de impacto podemos simplificar el
problema usando sus centros de masa.Si diferenciamos la ecuación 4 con respecto al tiempo tenemos.
 es la aceleración del centro de masa. Este centro de masa que
originalmente definimos obedece la segunda ley de Newton, así que.
es la aceleración del centro de masa. Este centro de masa que
originalmente definimos obedece la segunda ley de Newton, así que. Cuando el momento
es constante decimos que es conservado (lo que entra es lo mismo que
sale). Esta es una de las leyes más fundamentales de la física.
- Conservación de momento lineal: cuando la fuerza
externa neta de un sistema es cero, el momento total del sistema es constante.
Conservación de momento se mantiene no
importa cuántas partículas hay en el sistema ni como sea este movimiento. Este
aplica a sistemas que van desde átomos hasta colisiones de vehículos y hasta
galaxias. Esta ley es una de las más universales.
Ejemplos De
Conservación Del Momento
Cuando se dispara
una bala desde un arma, tanto la bala como el arma están inicialmente en reposo
con un momento total cero. Cuando se dispara la bala, acelera hacia adelante y,
como resultado de la conservación, el cañón del arma adquiere un impulso hacia
atrás. La cantidad de momento total antes de disparar una bala es cero y la
cantidad de movimiento total después también debe ser cero, lo que implica que
la cantidad de movimiento de la bala y la del cañón son iguales en magnitud,
pero en direcciones opuestas.
Energía Cinética
De Un Sistema
La conservación
de momento lineal nos dice que en un sistema de partículas los detalles
individuales de las partículas no afectan su velocidad o trayectoria sino el
movimiento de su centro de masa y este momento será el mismo al principio y al
final. Sin embargo, lo mismo no aplica para la energía cinética de un sistema.
Si vemos el caso de un petardo (un pequeño explosivo como fuegos artificiales),
este retiene el mismo momento lineal antes y después de explotar, pero su energía
cinética ha sufrido un cambio bastante obvio y drástico.
En la publicación
sobre “trabajo, energía y potencia” definimos la energía cinética como
Ahora pueden seguirnos y contactarnos a través de
Facebook, Twitter y correo electrónico.
- Facebook: https://www.facebook.com/JMDFisica
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com






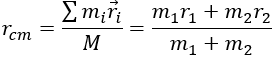



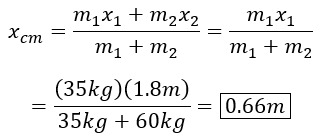







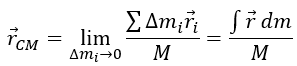

















Comentarios
Publicar un comentario