Solución a Problemas sobre la Fuerza
Una locomotora de ferrocarril de 37 Mg puede ejercer una fuerza de 0.7 MN. ¿A qué velocidad puede acelerar (a) por sí mismo y (b) cuando tira de un tren de 0.1 Gg?
Este es un problema bastante simple. Para calcular la aceleración usamos
la ecuación de la fuerza pero antes de eso debemos convertir las unidades.
37 Mg → 37 x 106 g
→ 37 x 103 kg
0.7 MN → 0.7 x 106
N → 7.0 x 105 N
0.1 Gg → 0.1 x 109 g → 0.1 x 106 kg → 1.0 x 105 kg
Para la parte (a) solo consideramos la masa del primer ferrocarril.
Estos resultados van alienados con las leyes de newton. Si aplicamos la
misma a dos objetos de masas diferentes la aceleración del objeto más pesado
será menor que la del objeto menos pesado.
En un concurso de lanzamiento de huevos, un estudiante encierra un huevo
de 72 g en un bloque de poliestireno. Si la fuerza sobre el huevo no puede
exceder los 2.3 N, y si el bloque golpea el suelo a 2.0 m/s, Cuánto debe
comprimirse la espuma de poliestireno al impactar?
Para conocer cuánto debe comprimirse la espuma de poliestireno es
simplemente calcular la diferencia en la distancia. Para ello debemos saber la
aceleración y como no hay dependencia de tiempo podemos usar una de las
ecuaciones de movimiento para ello. Primero usaremos la segunda ley de newton
para encontrar la aceleración.
72 g → 0.072 kg
Ahora que conocemos la aceleración podemos usar la ecuación del
movimiento que es independiente del tiempo.
Los términos x-x0 representa el cambio de distancia y cuando
se comprime la espuma de poliestireno. Así que la llamaremos Δx y vamos a
resolver la ecuación para encontrar su valor.
Asumiendo que la velocidad inicial es cero tenemos.
Usando la fuerza máxima permitida encontramos
cuanto la espuma de poliestireno se puede comprimir.
Un ascensor acelera hacia abajo a 1.7 m/s2. ¿Qué fuerza
ejerce el piso del ascensor sobre un pasajero de 75 kg?
Como el elevador acelera hacia abajo tenemos que esta es una aceleración negativa. Por lo tanto.
Si la comparamos con la fuerza cuando el elevador está en posición
estática.
Nos damos cuenta de que la fuerza es menor ya que cuando los objetos
caen ellos se sienten más ligeros.
¿Qué fuerza es necesaria para estirar un resorte 62 cm, si su constante
de resorte es 315 N/m?
Este caso es un simple ejemplo del cálculo de la fuerza de un resorte.
Para ello debemos convertir la distancia de centímetros a metro.
62 cm → 0.62 m
La fuerza de resorte es negativa pues el resorte prefiere estar es su posición original y toda fuerza aplicada disturba este estado.
Dos fuerzas actúan sobre una masa de 5.3 kg que experimenta una aceleración a = 0.73i-0.35j m/s2. Si una fuerza es -3.7i-5.2j N, ¿Cuál es la otra?
Dada la aceleración podemos encontrar la fuerza total. Una vez conocemos la fuerza total podemos sustraer una de las fuerzas para encontrar la otra.
Demuestre que la fuerza necesaria para mantener una masa m en una
trayectoria circular de radio r/2 con período T es π2mr/T2.
la aceleración de un movimiento circular es dada por.
Y la velocidad la podemos determinar por su circunferencia y el tiempo
que se toma en recorrerla, esto es el periodo T.
Así que sustituyendo podemos modificar la ecuación de la fuerza.
Como el radio dado es de r/2 reemplazamos este en la ecuación y
resolvemos.
A un disco de hockey se le da una rapidez inicial de 23 m/s. si se
detiene en 80 m, ¿Cuál es el coeficiente de fricción cinética?
En este problema queremos que la velocidad final sea cero. De la misma
manera el cambio de distancia es igual a 80 m y la velocidad inicial es de 23
m/s. usando la ecuación de movimiento independiente de tiempo podemos encontrar
la aceleración.
Ahora podemos calcular la fuerza cuando el disco de hockey se va a
detener siendo la fuerza de desplazamiento y la de fricción opuesta una con la
otra. Como la fuerza de fricción es determinada por µn, donde n es la fuerza
normal y esta vinculada con la superficie podemos llamarla mg, así que.
- Facebook: www.facebook.com/JMDFisica
- Twitter: @JMDciencias
- Correo: institutodecienciasjmd@hotmail.com
- Facebook: www.facebook.com/AprendeMatematicasJMD
- Blogger: aprendematematicasjmd.blogspot.com














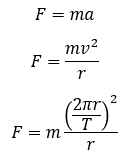






Comentarios
Publicar un comentario