La Fuerza Parte 4

Fuerzas de arrastre

    Las leyes de Newton nos enseñan que los objetos en caída libre experimentan la misma aceleración, sin embargo esto no es algo que vemos. Si dejamos caer una barra de hierro y una hoja de papel desde un edificio estos deberían llegar al suelo al mismo tiempo, pero no sucede así. ¿Acaso están las leyes de Newton equivocadas? Como vimos en el caso de movimientos en una superficie existe una fuerza contraria al movimiento que produce que los objetos se detengan, llamamos esta fuerza fricción. Analizando nuestro caso de la barra de hierro y el papel podemos asumir que debería existir una fuerza contraria a la caída de los objetos que esta relaciona con la superficie o densidad de los objetos que hace que estos no experimenten la misma caída y afecten las leyes de Newton. Llamamos a esta la fuerza de arrastre. 

    Cuando un objeto se mueve a través de un fluido (un gas o un líquido) experimentará fuerzas resistivas que llamamos fuerzas de arrastre. Un avión tiene una fuerza de empuje en la dirección de avance causada por el motor. También tiene una fuerza de arrastre en la dirección hacia atrás causada por las partículas de aire que aplican fuerza hacia atrás en el avión. Si el fluido a través del cual se mueve el objeto es aire, la fuerza de arrastre se llama resistencia del aire y su estudio se llama aerodinámica. Si el fluido a través del cual se mueve el objeto es agua, la fuerza de arrastre se llama resistencia al agua y su estudio se llama hidrodinámica. aunque la aerodinámica y la hidrodinámica pueden generalizarse más refiriéndose a fluidos gaseosos y líquidos respectivamente.

Gráficas comparativas de aceleración contra tiempo, velocidad conta tiempo, posición contra tiempo sin resistencia al fluido y con resistencia al fluido.

    La fuerza del fluido se ve afectada por varias cosas, como el área del objeto frente al fluido; cuanto mayor sea el área, mayor será la fuerza. La densidad del fluido; el agua y el aire tienen una densidad diferente y crean fuerzas diferentes. Experimentamos esto cuando intentamos correr en tierra versus cuando intentamos correr en el agua, uno es más denso y ejerce una fuerza mayor. La velocidad del objeto en el fluido y finalmente un coeficiente de arrastre que es una cantidad adimensional que se usa para cuantificar la resistencia de un objeto en un medio fluido. Combinando esto podemos obtener la siguiente ecuación.

    Donde C es el coeficiente de arrastre. ρ es el símbolo griego “rho” en esta ecuación se usa para indicar densidad. A es el área del objeto y v es su velocidad. Para reducir los efectos de la fuerza de arrastre vehículos de carreras son diseñados para ser aerodinámicos. Otro ejemplo de esto son las gotas de agua, la forma de los delfines y hasta el casco que usan los ciclistas.

Rapidez terminal

    Un objeto cae libremente desde el reposo, cuando el objeto cae experimenta una aceleración debido a la gravedad. En perfectas condiciones, el objeto seguirá acelerándose y su velocidad seguirá aumentando, pero las condiciones perfectas son raras de encontrar. El objeto comenzará a experimentar una fuerza de arrastre debido a la resistencia del aire que seguirá aumentando hasta que la fuerza de arrastre y la gravedad sean iguales. En ese punto, las fuerzas se equilibrarán y se cancelarán entre sí, por lo que el objeto no experimentará más aceleración y caerá con velocidad constante, a esto le llamamos la velocidad terminal.

Caída libre de una esfera y como la fuerza de arrastre la afecta a diferentes tiempo.

    Si tomamos el punto donde las fuerzas son iguales y manipulamos algebraicamente la expresión podemos encontrar una ecuación para la rapidez terminal.

Esto lo volveremos a ver cuándo estudiemos a más profundidad la dinámica de fluidos.

Fuerza en movimientos circulares

    Cuando un objeto se mueve en forma circular su posición está constantemente cambiando. Este cambio produce una aceleración hacia el centro del circulo aunque su velocidad sea constante (vea “movimientos en dos y tres dimensiones”). Como el vector de la aceleración apunta hacia el centro y la velocidad es constante el objeto experimenta una fuerza en la misma dirección que la aceleración lo que mantiene al objeto dando vueltas indefinidamente. Como ya habíamos descrito podemos encontrar la aceleración de un objeto que produce un camino circular de radio r dada una velocidad constante v como a = v²/r. así que la fuerza es.

    Esta fuerza se le llama fuerza centrípeta (del latín centrum que significa “centro”, y petere que significa “buscar”). Los satélites orbitan un planeta bajo este concepto al igual que un carro cuando enfrenta una curva en el camino. Esta aceleración también puede ser expresada usando el periodo T (el tiempo que le toma completar una vuelta). 

    Ejemplo. Un automóvil deportivo recorre una curva de radio R.  Si el coeficiente de fricción estática entre los neumáticos y la carretera es µ_s, ¿Cuál es la rapidez máxima v_máx con que el conductor puede tomar la curva sin derrapar?

    Para empezar debemos conocer todas las fuerzas que actúan sobre el automóvil. En este caso tenemos el peso del automóvil F_g y la fuerza normal n actuando en el eje vertical. Como el automóvil no tiene movimiento en este eje podemos decir que la fuerza neta es cero en el eje vertical. En el eje horizontal tenemos la fuerza de fricción f_f. El automóvil no se desliza hacia el centro del círculo, tampoco se desliza hacia afuera por lo que es fricción estática. Nombramos al eje vertical el eje y y nombramos al eje horizontal eje x. de modo que.

    La segunda ecuación nos dice que la fuerza normal es igual a la fuerza de gravedad mg y como habíamos definido anteriormente la fuerza de fricción estática es determinada por el coeficiente de fricción estática multiplicado por la fuerza normal. Así que para la primera ecuación tenemos.

Las masas se cancelan y podemos resolver la ecuación para encontrar la velocidad que por coincidencia nos dará la velocidad máxima para la fricción máxima.

Esta ecuación nos dará la velocidad máxima para un radio y coeficiente de fricción determinado.

    Con esto hemos cubierto lo básico a conocer sobre las leyes de Newton y las fuerzas. Nuestro próximo tema será sobre el trabajo y la energía. Ahora es su turno para practicar. Aquí les dejo unos ejercicios para practicar y en la próxima publicación estarán las respuestas.

1. Una locomotora de ferrocarril de 37 Mg puede ejercer una fuerza de 0.7 MN. ¿A qué velocidad puede acelerar (a) por sí mismo y (b) cuando tira de un tren de 0.1 Gg?
2. En un concurso de lanzamiento de huevos, un estudiante encierra un huevo de 72 g en un bloque de poliestireno. Si la fuerza sobre el huevo no puede exceder los 2.3 N, y si el bloque golpea el suelo a 2.0 m/s, Cuánto debe comprimirse la espuma de poliestireno al impactar?
3. Un ascensor acelera hacia abajo a 1.7 m/s². ¿Qué fuerza ejerce el piso del ascensor sobre un pasajero de 75 kg?
4. ¿Qué fuerza es necesaria para estirar un resorte 62 cm, si su constante de resorte es 315 N/m?
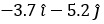5. Dos fuerzas actúan sobre una masa de 5.3 kg que experimenta una aceleración m/s². Si una fuerza es N, ¿Cuál es la otra?
6. Demuestre que la fuerza necesaria para mantener una masa m en una trayectoria circular de radio r/2 con período T es π²mr/T².
7. A un disco de hockey se le da una rapidez inicial de 23 m/s. si se detiene en 80 m, ¿Cuál es el coeficiente de fricción cinética?