Mecanica Classica: Movimientos en 1-D
La física siempre ha sido estudiada usando las matemáticas
como soporte para explicar cosas sobre el comportamiento del universo y la
naturaleza. La realidad como la percibimos es un mundo que definimos en tres
dimensiones espaciales que podemos definir como x, y, z; y una dimensión en
tiempo que definimos como t. Entender como el movimiento ocurre es la primera
parte del aprendizaje de la física y como este movimiento se relaciona con la
fuerza y la materia es el estudio de la mecánica, pero antes de que podamos
explorar la relación entre el movimiento y sus causas (la dinámica) , debemos
entender el movimiento. Esta rama de la mecánica que estudia el movimiento sin
importar su causa se llama cinemática.
Para empezar estaremos analizando una sola dimensión espacial, esta puede ser x, ó y, ó z, no importa cual, las ecuaciones serán iguales pero para hacer todo mas fáciles solo utilizaremos x para simbolizar una dimensión espacial de forma general. Este movimiento se le conoce como movimiento rectilíneo, pues la única gráfica que podemos crear en una dimensión es una línea recta.
El Desplazamiento
Si nos encontramos en nuestra casa y vamos a un restaurante a comer, ya no nos encontramos en el mismo lugar donde empezamos (nuestra casa), a esto le llamamos desplazamiento. Cuando un objeto cambia de una posición x1 hacia una posición x2 decimos que el objeto se ha desplazado y la distancia recorrida es la diferencia entre la posición x1 y la posición x2.
Δx = x2 - x1
(1)
El símbolo Δ se usa para indicar diferencia (resta). La distancia es una de las unidades fundamentales del sistema de unidades SI y se mide en metros (existen otras unidades de medida como la pulgada, pie, milla, … pero el estándar esta con el sistema SI), y es conocida como un vector (ya que contiene dirección y magnitud; para mas informaciones sobre vectores consulten aquí). Como vector podemos expresarlo de la siguiente manera.
(existen diversas formas de expresar los vectores pero la
idea es que cuando veamos un símbolo encima de la expresión debemos identificar
que es un vector con excepciones del promedio que en estadística es simbolizada
por una barra arriba de la expresión). Como estamos tratando en 1-D
probablemente solo lo trataremos como una magnitud, cuando hablemos de más
dimensiones veremos la importancia de los vectores.
El desplazamiento en si es bastante simple de entender y
calcular pero cuando agregamos tiempo las cosas cambian un poco. Supongamos que
nos trasladamos desde nuestra casa a un restaurante y nuestro vecino también
sale de su casa hacia el mismo restaurante al mismo tiempo. El restaurante esta
a 15 km de distancia de nuestra casa y nos toma 30 minutos llegar allá. A
nuestro vecino la misma distancia le toma 15 minutos. Aunque la distancia
recorrida para nosotros y nuestro vecino es la misma, el tiempo que nos toma
hacer el recorrido no es igual. Este tipo de problemas se resuelven usando la
velocidad.
La Velocidad
La velocidad v la podemos definir como la diferencia entre
la distancia recorrida dividida por el tiempo que se toma en recorrerla y la
podemos expresar así.
Cuando la velocidad depende del intervalo de tiempo elegido
nos referimos a la velocidad media o velocidad promedio donde los únicos puntos
de interés son la posición inicial y la posición final al igual que el tiempo
inicial y el tiempo final:
Donde la ultima expresión es la forma en que cálculos
presenta cambios infinitesimales (muy pequeños). Esto no se debe confundir con
la rapidez. En términos generales cuando hablamos de la velocidad hablamos de
todos los términos en general (distancia dividida por el tiempo), pero en caso
de que sea necesario cuando hablamos de la rapidez nos referimos a la distancia
total dividida por el tiempo transcurrido. Mientras la velocidad media se
preocupa simplemente por el punto de inicio y el punto final, la velocidad
instantánea se centra en un solo momento y la rapidez se enfoca en el total.
Otra forma de verlo es cuando hablamos de velocidad nos referimos al vector y cuando
hablamos de rapidez nos referimos a un escalar.
Ejemplo de velocidad y rapidez:
para conseguir un vuelo barato de Guatemala a El Salvador -
una distancia de 1000 km - tienes que conectar en México, 700 km al norte de El
Salvador. El vuelo a México toma 2.2 horas, luego tiene una escala de 30
minutos y luego un vuelo de 1.3 horas a El Salvador. ¿Cuáles son su velocidad y
rapidez promedio en este viaje?
Nota: Los números de este problema son ficticios y no describen la distancia real entre estos países.
Comienzas en Guatemala y terminas en El Salvador con un desplazamiento de 1000 km, independientemente de lo lejos que hayas viajado realmente. El tiempo total para los tres segmentos es Δt = 2.2 h + 0.5 h +1.3 h = 4.0 h entonces la velocidad promedio es
Ejemplo de velocidad instantánea y velocidad media
La altitud de un cohete en el primer medio minuto de su
ascenso viene dada por la expresión x = bt2, donde la constante b es 2.90 m/s2 .
Para encontrar la velocidad instantánea podemos usar la forma infinitesimal de cálculos para calcular su derivada de la ecuacion 4.
Asumiendo que el cohete inicia en reposo (x1 = 0; t1 = 0).
La comparación con nuestro resultado anterior muestra que la
"velocidad promedio es exactamente la mitad de la velocidad
instantánea".
(los ejemplos han sido tomados de Essentials University
Physics 2nd edition por Richard Wolfson)
La aceleración
Así como presentamos un objeto que puede cambiar su posición
con el tiempo y producir velocidad, la velocidad también puede cambiar con el
tiempo. Definimos como aceleración al cambio de velocidad Δv en un intervalo de
tiempo de tiempo Δt.
Tanto en el caso de la velocidad como en la aceleración ambos
son vectores y se pueden calcular su media e instantánea.
En una dimensión la aceleración puede ir en dirección de la
velocidad u opuesta a ella. En el primer caso decimos que su velocidad aumenta
mientras que en el segundo decimos que su velocidad disminuye. Como la
aceleración es el cambio de velocidad con el tiempo. Unidad de media es
distancia/tiempo/tiempo o distancia/tiempo2
Gráficas de
velocidad y aceleración
En la ecuación 2 tenemos a la variable x y t como variables independientes mientras v es una variable dependiente es decir que la gráfica que haremos sera usando los ejes x y t, y nos darán información sobre v. Si reorganizamos la ecuación tenemos vΔt = Δx para hacerla ver un poco mejor vamos a quitar el símbolo Δ → vt = x. Esta ecuación aunque no lo parezca la hemos visto antes en la siguiente forma: y = mx + b. Esta es la ecuación de la pendiente. Si sustituimos y por x, y x por t, y dejamos b al origen (b = 0) entonces tenemos x = mt. y si la comparamos veremos que m = v donde m es la pendiente. Esto nos indica que la pendiente de la gráfica x-t es v.
No es coincidencia que la formula para calcular la pendiente sea igual que la formula de la velocidad
La velocidad puede cambiar dentro de una misma gráfica. Todo
depende del intervalo que se tome para medirlo.
Cuando La velocidad es positiva el movimiento es en la dirección +x; cuando la velocidad es negativa el movimiento es en la dirección -x; cuando la tangente es horizontal la pendiente y la velocidad son cero.
Para la aceleración es la misma idea que la velocidad donde
la gráfica sera de v-t. en este caso la pendiente sera la aceleración a.
También podemos conocer la aceleración de un cuerpo a partir de una gráfica de posición y tiempo ya que a = dv/dt y v = dx/dt.
Aceleración constante
El movimiento acelerado mas simple a estudiar es el
movimiento con aceleración constante donde la velocidad cambia al mismo ritmo a
lo largo del movimiento. Un buen ejemplo
de esto es la caída libre donde podemos ignorar los efectos del aire. Si tomamos un objeto que el tiempo
de inicio t1 = 0 y una velocidad inicial v0 y aceleración
constante a. después de un tiempo t2 = t experimenta una velocidad v
distinta a v0. Como su aceleración no cambia, su velocidad
media e instantánea son iguales. Así que podemos decir
Esta ecuación nos dice que la velocidad cambia de valor
inicial agregando la cantidad del producto de su aceleración y el tiempo.
La gráfica de a-t en aceleración constante es una linea
horizontal ya que el valor de la aceleración a no cambia. La gráfica de velocidad
contra tiempo v-t tiene una pendiente constante, por lo que es una linea recta.
Con aceleración constante la
velocidad cambia continuamente, por lo que para determinar la velocidad
promedio en un intervalo solo necesitamos el punto inicial y el punto final.
Para la
velocidad promedio con un tiempo inicial t = 0 hasta un tiempo arbitrario t
podemos escribir la velocidad promedio en términos de desplazamiento.
Para ver la
simplificación vamos a llamar vinicial = v0 pues es la
velocidad en el tiempo t = 0; y vfinal = v pues es la velocidad en
tiempo t que nosotros ya habíamos encontrado anteriormente en la ecuación 9.
En la
ultima ecuación vemos que sin aceleración (a = 0) la ecuación se convierte en
una ecuación linear con una pendiente igual a v0 pero si la
aceleración es constante el termino ½ at2
Hasta ahora las ecuaciones que hemos derivado dependen del tiempo pero Que tal si tenemos un problema donde no sabemos
el tiempo que se toma para el objeto acelerar o cambiar de velocidad?
Si tomamos la ecuación 9 y la resolvemos por el tiempo tendremos
Esta nueva expresión la podemos usar en la ecuación 12 para sustituir el tiempo.
Como sabemos que (a + b)(a - b) = (a2 - b2)
tenemos
Las Ecuaciones 9, 12, 13 y 14 se les conoce como las
ecuaciones de movimiento para aceleración constante ya que con ellas se puede
resolver cualquier problema relacionado a la posición, velocidad y aceleración.
No es necesario memorizarlas pero saber de donde provienen y como usarlas es
esencial.
Un avión de
pasajeros aterriza a 270 km/h. Luego, el avión desacelera (experimenta una
aceleración opuesta a su velocidad) a 4.5 m/s2. ¿Cuál es la
longitud mínima de la pista sobre la que puede aterrizar esta aeronave?
Este es un problema de una dimensión que podemos resolver usando la ecuación 14 pues no tiempo ha sido indicado. Como queremos saber la longitud mínima de la pista para aterrizar la velocidad final debe ser cero. También podemos sustituir la diferencia x - x0 = Δx que es lo que deseamos y resolvemos nuestra ecuación para ello.
Como la magnitud de la velocidad y la aceleración no son
iguales debemos convertirlas para que concuerden.
Caída libre
El ejemplo mas conocido de movimiento con aceleración (casi)
constante es la caída bajo la influencia de la atracción gravitacional. La
aceleración de la gravedad es conocida en física por la letra g y tiene un
valor de 9.81 m/s2 alrededor de la superficie de la Tierra. Como la gravedad
hace que los cuerpos caigan, por lo
general se describe como -g aunque esto es opcional y podemos asignarle un
valor positivo. En el siglo IV a.C., Aristoteles pensaba que los objetos
pesados caían con mayor rapidez que los ligeros en proporción a su peso.
Diecinueve siglos después esto se comprobó ser falso por Galileo Galilei cuando
afirmo que los cuerpos caían con una aceleración constante e independiente de
su peso. Este modelo teórico requiere que la superficie sea uniforme y los
efectos como la rotación de la tierra y el aire sean ignorados se le conoce
como caída libre (aunque también encompasa el movimiento ascendente).
Podemos usar las ecuaciones de movimiento para aceleración
constante cambiando la aceleración por la gravedad a = g.
Ejemplo de caída libre
Se deja caer una moneda desde el edificio Empire State. La
moneda cae libremente a partir del reposo. Calcule su posición y velocidad
después de 1.2 s, 2.5 s y 3.0 s.
El cuerpo inicia en reposo indicando que x0 = 0;
v0 = 0 en la cima del edificio. Como la moneda se deja caer y
desciende hasta el piso. elegimos la coordenada -y para expresar la posición.
Usando la ecuación 9 podemos encontrar la velocidad en cada instante.
Para determinar la posición podemos usar la ecuación 13, sustituyendo a = -g








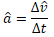



























Comentarios
Publicar un comentario